
Een verdunning berekenen? gratis online oefenen
Het werk in de zorg komt je niet zomaar aanwaaien. Dat blijkt ook wel uit de
moeilijkheidsgraad van de verschillende toetsen die je terugziet tijdens de opleiding
verpleegkunde. Een van de vakken waar veel mensen moeite mee hebben, is medisch
rekenen. Niet alleen komt dit doordat er veel gewerkt wordt met hoofdrekenen en
basisregels van rekenvaardigheid, ook moet je veel theorie kennen die jou de basis geven
om de juiste berekeningen te maken. Een van de dingen waar je mee te maken krijgt tijdens
het vak is een verdunning berekenen. Onderstaande informatie laat jou zien wat een
verdunning is en hoe je deze kunt gaan berekenen.
Inhoudsopgave
Een verdunning berekenen binnen medisch rekenen
De basiskennis van een verdunning berekenen
Een verdunning berekenen aan de hand van voorbeelden
Verder voorbereiden op de toets
Een verdunning berekenen binnen medisch rekenen
Medisch rekenen kent veel verschillende onderwerpen. Dit begint al bij de basiskennis van
rekenvaardigheid. Je hebt de algemene kennis en vaardigheden nodig om op de juiste
manieren aan de slag te gaan met de berekeningen binnen de praktijk. Niet alleen moet je
weten hoe je verschillende sommen uit je hoofd kunt oplossen, ook zijn er verschillende
rekenregels die door elkaar gebruikt moeten worden. Jouw opleiding begint daarom bij de
basis en breidt zich steeds verder uit.
Na de basis komen verschillende rekenvaardigheden uit de praktijk. Zo moet je kunnen
rekenen met medicijnen, infusen, zuurstof en concentraties. Bij laatstgenoemde komt een
verdunning berekenen om de hoek kijken. Je moet namelijk eerst de concentraties weten en
weten hoe deze berekend worden voordat je aan de slag kunt gaan met het maken van een
verdunning. Door middel van verschillende oefeningen word je door de theorie geleid,
beginnend bij wat een concentratie precies is en hoe je deze uit kunt rekenen. Nadat de
basis is uitgelegd, ga je door naar het rekenen met Mol en millimol. Veel medicijnen hebben
namelijk op het etikel het aantal millimol per milliliters staan. Pas wanneer je deze gedeeltes
door bent gekomen, ga je aan de slag met verdunnen van bepaalde producten en kun je de
juiste hoeveelheden samenstellen.
De basiskennis van een verdunning berekenen
Een verdunning berekenen gaat aan de hand van een aantal stappen. Je hebt namelijk een
bepaalde hoeveelheid nodig en er is een bepaalde hoeveelheid aanwezig. Je moet daarom
goed bepalen wat je wel en niet weet. In feite is een verdunning niet meer dan een kleine
hoeveelheid nemen van een bekende concentratie om die met gedestilleerd water te
mengen. Van hieruit ontstaat een nieuwe concentratie. Aan de hand van wat je wel en niet
weet, kun je uiteindelijk bepalen hoeveel er nodig is.
Daarbij is het goed om eerst te bekijken wat een concentratie is. Een concentratie geeft een
verhouding aan tussen bepaalde stoffen. Zo zit er een bepaalde stof voor een bepaald deel
in de andere. Dit wordt vaak aangegeven in procenten en de verschillende eenheden
vormen samen een geheel. Zo kunnen er een aantal milliliters in 100 liter zitten, maar ook grammen in liters en grammen in kilogrammen. Neem bijvoorbeeld onze lucht. Per 100 liter
lucht zit er 78 stikstof, 21 zuurstof en 1 andere gassen in. Dit houdt in dat onze lucht voor
78% uit stikstof en 21% uit zuurstof bestaat. Uiteraard is dit een eenvoudig voorbeeld. In
sommige gevallen wordt er niet met hele getallen gewerkt.
Vereenvoudig de eenheden aan de hand van de vraagstelling
Het kan ook voor komen dat er niet met procenten maar met andere eenheden gewerkt
wordt. Dit komt vaak voor bij medicijnen. Op het etiket staan de werkzame deeltjes
aangegeven. Deze werkzame deeltjes worden aangetoond met Mol. Het is hierbij goed om
te weten dat 1 Mol 6 x 10 23 betekent. Een millimol is hierdoor 6 x 10 20 . Je kunt hier
eenvoudiger mee gaan rekenen, doordat je weet waar de eenheid voor staat. Zo kan er op
het etiket staan dat 10 mL 1,54 mmol van een bepaalde stof bevat. Deze stof weegt 0,9
gram. Deze grammen heb je uiteindelijk nodig om tot de goede oplossing te komen.
Een verdunning berekenen betekent ook dat je met verschillende eenheden aan de slag gaat
werken. Zo kan er bij het een iets in procenten staan, bij de andere in mmol en weer bij een
andere in grammen. Voordat je een berekening op gaat lossen moet je er echter wel voor
zorgen dat je alle eenheden gelijkgetrokken hebt. Hierbij komt jouw basiskennis van het
rekenen weer kijken. Je hebt namelijk ook eenheden om leren zetten, waardoor je het voor
jezelf eenvoudiger kunt maken. Denk hierbij aan 100 mL omzetten in liters of grammen in
kilogrammen. Door dit voor jezelf direct te doen als in de vraag met liters gewerkt wordt,
kun je ervoor zorgen dat je jouw berekeningen niet op een foutieve manier uit gaat voeren.
Een verdunning berekenen aan de hand van voorbeelden
Een verdunning berekenen gaat dus niet zonder de theorie die hieraan voorafgaat. Zonder
de theorie ga je bepaalde logica over het hoofd zien, waardoor je de verkeerde
hoeveelheden met elkaar gaat mengen. Echter kun je de berekeningen ook niet maken als je
nog nooit vragen hebt gezien voor de toets. Je moet daarom altijd zoveel mogelijk oefenen
om tot het juiste antwoord te kunnen komen. Onderstaande voorbeelden geven jou een
beter beeld bij wat je kunt verwachten en op welke manier je de verdunningen kunt gaan
berekenen.
We beginnen hierbij eenvoudig. Je moet als eerste weten dat wanneer je een verdunning
berekenen gaat, je dit in verschillende stappen uit moet gaan voeren. De eerste stap is om te
kijken hoeveel milligram of milliliter je van de stof nodig hebt in de gewenste concentratie.
Dit is dus altijd de eerste berekening die je gaat maken. De tweede stap is om te berekenen
hoeveel er aanwezig is. Dit wordt altijd gedaan in milliliters. Je moet deze milliliters op
papier hebben staan om ze uiteindelijk aan te kunnen vullen tot de gevraagde hoeveelheid.
Bereken eerst wat je nodig hebt
Denk hierbij aan een glucoseoplossing van 10%, waarbij je 200 mL moet maken van 5%. 10%
betekent in feite dat er 10 gram aanwezig is in 100 mL. Om hier 200 mL van te maken, moet
je deze aanvullen met gedestilleerd water. Op deze manier ontstaat er een verdunning. Ook
zou het kunnen dat er van een oplossing van 10% een oplossing van 3% moet worden
gemaakt. Je hebt nog altijd te maken met de 10 gram per 100 mL, maar moet er dit keer 500
mL van maken. Je moet een verdunning berekenen aan de hand van deze gegevens. Ook
hier kijk je eerst weer wat je al weet. Er is 10 gram op 100 mL aanwezig. Je hebt maar 3 gram nodig. Bereken daarom eerst wat er nodig is om 500 mL te maken. Om van 100 mL 500 mL
te maken, moet je deze vermenigvuldigen met 5. Daarom moet ook de 3 gram
vermenigvuldigd worden met 5. Je hebt dus 15 gram nodig voor de gewenste oplossing.
Daarna kun je door met de berekening hoeveel je van de aanwezige oplossing nodig hebt.
De 10 gram op 100 mL moet veranderd worden naar 15 gram. Dit is in feite niets meer dan
een simpel rekensommetje, waar jouw basisvaardigheden weer om de hoek komen kijken.
Om van 10 gram naar 15 gram te gaan, moet je 10 vermenigvuldigen met 1,5. Daarom moet
je 100 mL ook vermenigvuldigen met 1,5. Hieruit blijkt dat je 150 mL nodig hebt voor de
nieuwe oplossing. Je moet dus 150 mL pakken en deze aanvullen tot 500 mL om tot een 3%
oplossing te komen.
Op de afdeling waar je werkzaam bent is een glucoseoplossing van 40% aanwezig. Je hebt 20
mL van 4% nodig. Hoeveel milliliter oplossing en hoeveel milliliter gedestilleerd water heb je
nodig om de gewenste oplossing te maken?
Denk bij deze vraag eerst terug aan de basis. 4% betekent volgende basisbeginselen dat er
4mg in zit. Dit staat gelijk aan 8 mg op 20 mL. 40% is 40mg op 10 mL, wat ook weer gelijk
staat aan 8 mg op 2 mL. Je moet daarom 2 mL van 40% pakken en deze aanvullen tot 20 mL
met water.
Als laatste bereken je het aantal milliliter
Actisan 5L wordt in ziekenhuizen als desinfectiemiddel gebruikt om bacteriën en gisten te
bestrijden. Deze oplossing bevat 55 procent actief chloor. Op een patiëntenafdeling is 3 liter
nodig met 30 procent actief chloor. Hoeveel milliliter heb je nodig om de gewenste oplossing
te maken?
Een verdunning berekenen gebeurt altijd op basis van wat je nodig hebt. Je moet daarom
eerst deze informatie eruit halen en berekenen. In het verhaal zie je staan dat je een
oplossing met 30 procent nodig hebt. 30 procent staat gelijk aan 30 gram per 100 mL. Er is 3
liter nodig van deze oplossing. Je moet daarom 100 mL omzetten naar 3000 mL. Dit is 30
keer zoveel. Je moet daarom ook 30 keer zoveel milligrammen hebben. Jouw benodigde
aantal wordt in dit geval 900 gram.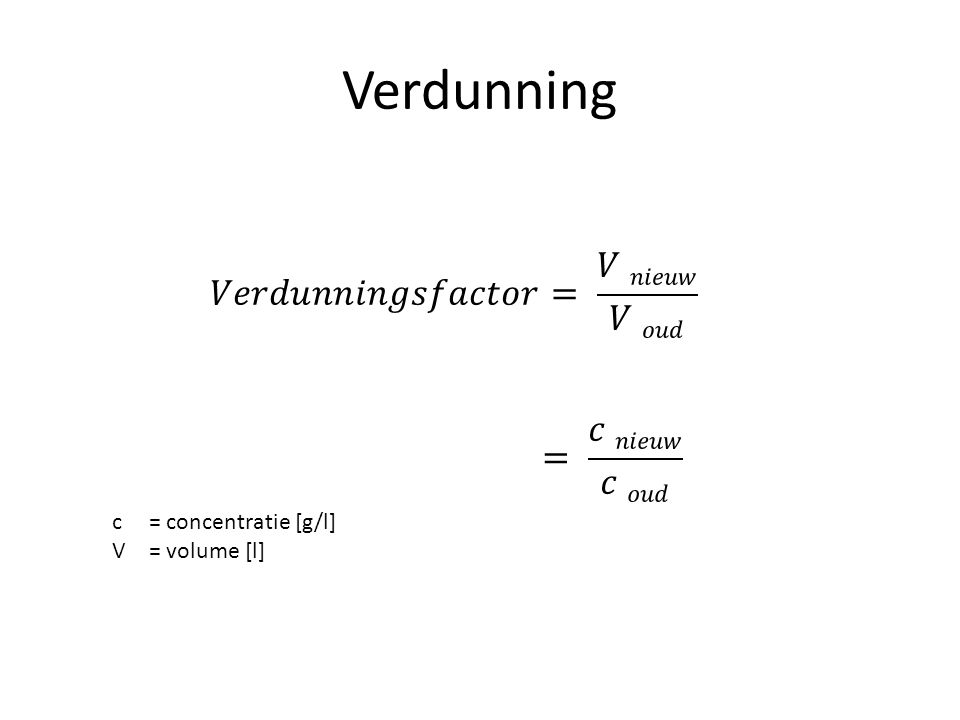
Daarna ga je kijken naar wat er aanwezig is. Je ziet dat er een oplossing met 55 procent
beschikbaar is. Dit staat gelijk aan 55 mg per 100 mL. Van hieruit kun je gaan rekenen. Je
kunt ervoor kiezen om eerst terug te rekenen naar 1, maar ook om direct te kijken naar hoe
vaak 55 in 900 gram past. In dit geval is het eenvoudiger om eerst terug te rekenen. Er zit 1
gram per 1,81 mL in de oplossing. Je hebt 900 gram nodig. Door deze op te schrijven en de
1,81 x 900 uit te rekenen kom je tot het goede antwoord. Dit is wellicht lastig om uit je
hoofd te doen. Als je dit intypt in jouw rekenmachine komt er uit jouw antwoord 1636 mL. Je
moet dus 1636 mL pakken en deze aanvullen tot 3000 mL. Je had immers 3 liter aan vloeistof
nodig om te desinfecteren.
Niet alleen een oplossing voor een dag
Gedurende 7 dagen wordt er intensief schoongemaakt op de patiëntenafdeling. Wederom is
er een oplossing van 55 procent aanwezig op de afdeling. Per dag is er 2,5 liter van 22
procent nodig. Hoeveel liter van 55 procent moet je hebben om voor alle dagen
desinfectiemiddel op voorraad te hebben? Ook hier weer ga je eerst de verdunning berekenen aan de hand van wat je nodig hebt. Per
dag is er 2,5 liter van 22 procent nodig. 22 procent staat gelijk aan 22 mg per 100 mL. Dit
schrijf je dus als eerste op. 2,5 liter is 2500 mL. Je moet daarom het aantal milligrammen
vermenigvuldigen met 25. 22 x 25 = 550. Er is dus 550 gram nodig voor de gewenste
oplossing.
Met deze berekening ben je er echter nog niet. We gaan nu kijken naar wat er aanwezig is,
om te bepalen hoeveel milliliter er uiteindelijk nodig is per dag om het ziekenhuis te kunnen
reinigen. Je hebt een 55 procent oplossing tot jouw beschikking. Er zit 55 gram per 100 mL
in. Je hebt uiteindelijk 550 gram nodig. Dit is een vrij eenvoudige som. 550 / 55 = 10. Je kunt
daarom 100 mL x 10 = 1000 mL uitrekenen. Er is per dag een liter van 55 procent oplossing
nodig. Er moet dus minstens 7 liter in voorraad zijn om alles naar behoren schoon te kunnen
maken.
Verder voorbereiden op de toets
Als je jezelf nog beter voor wilt bereiden op de medisch rekenen toets kun je het beste
zoveel mogelijk oefenvragen maken. Door iedere dag intensief bezig te zijn met de stof kun
je iedere verdunning berekenen zonder dat hier veel onnodige fouten bij gemaakt gaan
worden. Deze fouten kunnen in het werkveld immers fataal zijn, waardoor je ervoor moet
zorgen dat je jouw kennis iedere dag weer meer uitbreidt. Jouw werkgever zal hier veel
waarde aan hechten en jouw patiënten zullen te allen tijde de juiste hoeveelheden
toegediend krijgen.

